It is a known fact that quality cannot be tested into a product, but must be created with a suitable product design. Likewise, the safety and reproducibility of processes cannot be achieved through validation. Validation can only prove whether a process is suitable or not. The suitability itself results from the careful development and optimisation of the process. This should achieve a degree of understanding of processes which will allow them to be predictably formulated. The use of process-analytical technologies and the establishment of a design space, among other things, are useful for this. The following chapter illustrates the significance of these principles for process validation.

1 Process development

Process validation is designed to prove the suitability of processes. Suitability must be ensured by the design of the process. The development of a suitable process design is part of the pharmaceutical development and must be described in the application file for marketing authorisation of a new drug product.

The principle that quality cannot be tested into a product, but that it results from a suitable design has been applied in the European approval system for a long time now. In November 2005, the ICH (International Conference on Harmonisation) launched the ICH M4 document, which describes a standardised format for application files for marketing authorisation. But even before this, applicants were required to describe the pharmaceutical development of the drug product in the application file. Today, in Section 3.2.P.2 of the CTD, details are to be given about the pharmaceutical development, especially the selection and optimisation of the manufacturing process, and its critical aspects are to be presented.

Among other things, the development phase of a drug product serves to determine the optimum design of the manufacturing process and to verify which control and checking equipment is required to ensure the process runs smoothly. Experience from the development phase should make it possible to determine the critical parameters of the process. There are various methods for doing this which can also be applied in the subsequent process validation phase, so that it is acceptable to refer back to the results. The fishbone and Pareto analyses should be mentioned as examples here (see figure 1).

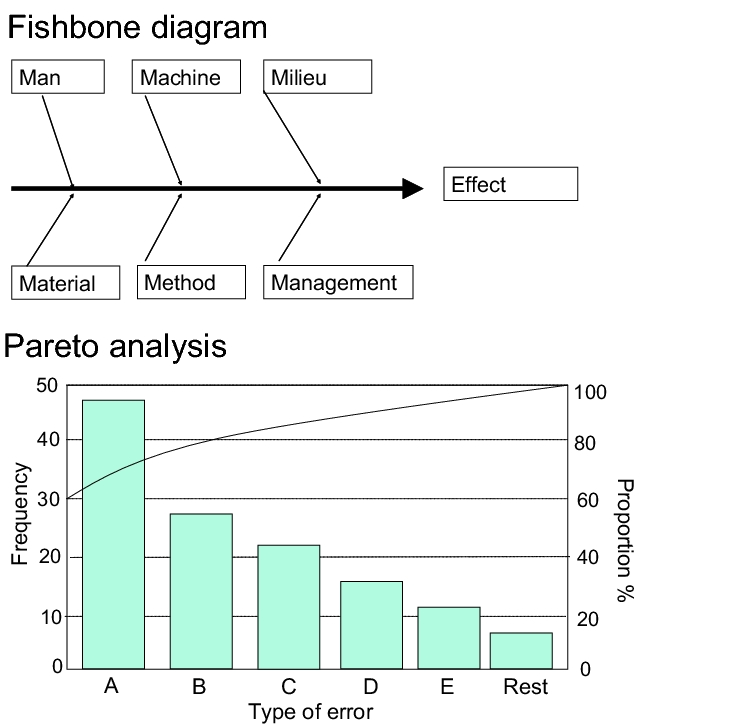The fishbone diagram (cause-and-effect diagram) can be used to analyse a defined effect (e.g. fault) for its causes. The effect is entered as the "fish head", the individual "fishbones" are the main influencing variables, which can be further differentiated into secondary influencing variables. Possible solutions to the most likely disturbance variable are sought and implemented (see also chapter 10.D.2 Preparation using a fishbone diagram).

Pareto analysis is a way of setting priorities in complex situations which result from a large number of problems and causes of failure. The greatest, most significant or most expensive problem is logically approached first. The Pareto analysis shows the influencing factors relevant to a situation in order of their size and significance. It often turns out that many of the known problems are insignificant, but that small problems are still important.

During the improvement phase, the batch consistency is documented, following the enlargement of the laboratory scale to approximately 1/10 of the subsequent commercial scale. The efficiency of the process is technically and economically optimised (see chapter 16.B.7 Process optimisation: Basic principles for process validation).

The information obtained as part of the pharmaceutical development forms the basis for subsequent risk management of the product quality (see chapter 10 Risk Management). The development of a manufacturing procedure and its ongoing development by means of a continuous improvement process throughout the entire product life cycle are the foundations upon which a deeper understanding of the process can be built.

Whereas the examination of the critical factors of a manufacturing process requires a certain minimum understanding of the process, other approaches, such as multivariate data analysis (MVDA, see chapter 4 Multivariate Data Analysis (MVDA)), statistical design of experiments (DoE, see chapter 3 Statistical Design of Experiments (DoE)) together with process analytical technologies (PAT, see chapter 7.J Process Analytical Technology (PAT)) go even further. It is generally recognised that these tools can be used to better explain the relationship between the variabilities of a process or starting material and the quality of the final product. They are used to create a basis for optimum process checking and process control which ensures that the final product automatically has the required quality.

2 Design space

The design space concept (for a definition, see figure 2) is a modern approach for increasing the flexibility of the production process. Classical manufacturing processes are routinely characterised by process parameters (e.g. temperature, time, pressure, stirring speed) for which acceptance criteria with upper and lower limits for production are defined. The process must be controlled within these limits so that a product is obtained which conforms to specifications. These limits are usually derived from the proven acceptable ranges (PAR) during development, i.e. the limits above and below which the product is likely to be defective. The process is defined in this way and implemented within these fixed limits. Such rigid processes are only able to adapt to variable requirements, e.g. due to various starting material qualities or environmental conditions.

Often, the process parameters themselves interact with each other. For example, to dry a product, either a high temperature and a short drying time or a lower temperature and a relatively longer drying time can be worked with. If you also work with a variable air volume flow to support the drying process, the aforementioned parameters can be adapted accordingly, i.e. the positions of the upper and lower limits are moved depending on the parameters with which they interact. Based on this knowledge of the multifactorial dependencies, multidimensional spaces which characterise a multifactorial parameter range in which a specification-compliant product is contained can be graphically and mathematically represented (design space). The advantage of the design space concept is obvious: variable characteristics of a starting material (e.g. humidity, particle size, surface) can be balanced within the design space by simultaneously varying several parameters so that the quality of the end product remains constant. Process analytical technologies (see chapter 4 Multivariate Data Analysis (MVDA)) are useful for measuring and controlling these parameters.

The design space must also be checked for suitability, in the same way as the classical acceptance criteria during the validation. However, further tools are used to verify a design space, e.g. statistical design of experiments (see chapter 3 Statistical Design of Experiments (DoE)) and multivariate data analysis (see chapter 4 Multivariate Data Analysis (MVDA)).

Data from the research and development phase and experience from production should enable a deeper understanding of the process. Investigations of a wider range of materials, sequences of operations and process parameters are required for this in order to build up the required knowledge. These findings may result from experiments from statistical designs of experiments, data from PAT applications or existing production experience. A value space for a special manufacturing process is defined based on the necessary process parameters and within the limits of which the process runs stably. If the correct limits are selected, the number of change notifications required can thus be reduced. The selection of the correct process parameters is therefore an indispensable requirement. Process analysis thus has a particular significance in the implementation of the design space concept. PAT tools are often used for this (see chapter 4 Multivariate Data Analysis (MVDA)), but it is not necessarily always the case.

Design space descriptions generally contain a particularly large number of variables with the interesting information hidden in combinations of variables. It is therefore nearly impossible to discover the most important information and correlations in the data visually or using traditional methods. Even if only two settings are to be investigated for eight factors in a process (known as screening), it would require 2⁸ = 256 trials. For three settings per factor, the requirement would be 3⁸ = 6561 experiments. From this, it is obvious that a pure trial and error approach only has a very low chance of achieving anywhere near the ideal development conditions.

In order for a design space to be determined, considerable amounts of information must first be gathered using practical measurements and theoretical model calculations. This data also covers parameter ranges which yield specification-compliant and non-specification-compliant products. This range is known as the knowledge space (see figure 4).

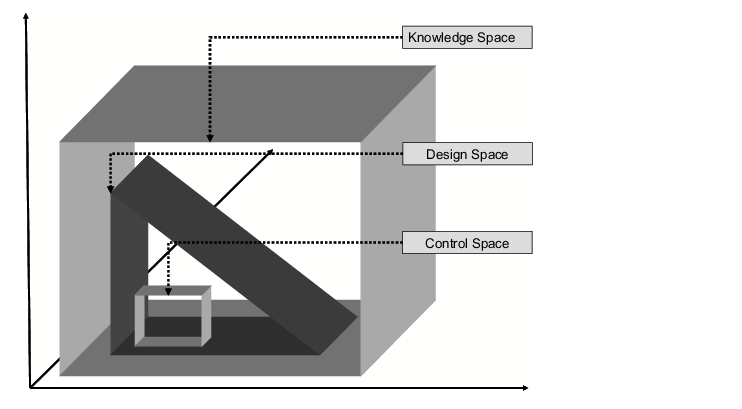Within the knowledge space, a range is determined within which a specification-compliant product is obtained. This range is called the design space. In routine production, the process is controlled such that it runs within the design space. For this, a smaller range, the control space, is generally established.

The fact that a process can be run within the defined design space and thus deliver a specification-compliant product is typically verified with a defined collection of batch-specific product and process information, the process signature (see figure 5).

The process signature is obtained from process-analytical at-line, on-line or in-line measurements (see figure 7.J-1). The variety of dimensions in a design space are typically dependent on each other. There are relationships - so-called correlations - between categories in different dimensions. They describe how design alternatives fit with each other, i.e. they indicate advantageous or disadvantageous combinations of design decisions.

3 Statistical Design of Experiments (DoE)

In order that the design space concept can be effectively implemented, various tools are required that support both the creation and the manipulation of design-space descriptions. Design-space descriptions are therefore usually based on software-assisted statistical design of experiments.

Pharmaceutical processes are often dependent on a relatively large number of variables (e.g. temperature, time, humidity, pressure, particle size). It is practically impossible to test every combination of variables during process development in order to determine the relevant correlations between the individual variables.

Even where there is enormous time pressure for developing new formulations, DoE (see figure 6) can release enormous potential. It uses a minimal number of experiments to provide an empirical process model for the interrelationship between the control and disturbance variables in the process and the resulting product and process characteristics. An appropriate system analysis of the process parameters, their adjustment ranges and the selection and measurability of the target variables must be carried out.

In contrast to conventional process development using the variation of parameters for each experiment, DoE advocates virtually maximising the "experiment space" and hence varying several factors at the same time.

As part of the DoE, experiment designs are created which take account of the following:

• Number of factors to be investigated (at least two)
• Type of factors to be investigated:
• qualitative features: nominal (e.g.: yes/no or good/bad) or ordinal (sequential relationship, e.g.: grouping, >, =, <)
• quantitative features: continual (infinite value range, e.g. temperature measurement values or diameter of a tablet) or discrete (integer observed values, e.g. manufactured packages/hour or deviations/batch)
• Inclusion of existing information
• Determination of the desired accuracy and reliability of the evidence

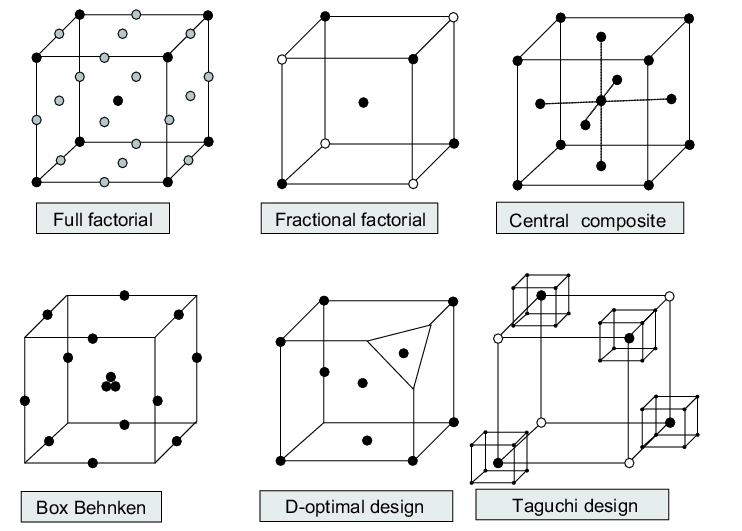
Conventional designs in DoE (see figure 6) are

• Full factorial designs
• Fractional factorial designs
• Central composite designs
• Box-Behnken designs
• D-optimal design
• Taguchi designs
• Mixed designs

In particular, fractional factorial designs (so-called screening designs) provide the possibility of significantly reducing the number of experiments. Results from screening designs can also be transferred to a subsequent series of experiments with less investigated factors, known as response surface designs. Response surface designs are used to determine and then optimise non-linear interrelationships.

4 Multivariate Data Analysis (MVDA)

Large data records with several variables can be reliably interpreted with multivariate data analysis (MVDA). In the MVDA, the probabilistic criteria of univariate statistics are joined by added algebraic criteria for reducing the dimensionality of the feature or sample space and by geometric criteria for suitable graphical representations. It should be noted that the problems of estimating parameters and inferring the whole from the random sample that are prominent in univariate statistics are generally secondary concerns in multivariate statistics and data analysis. In this respect, multivariate statistics and data analysis can only be considered as a generalisation of univariate statistics and data analysis.

Multivariate data is organised in a matrix, i.e. as a data table, that has as many rows as the number of objects/samples being investigated and as many columns as the features/variables being measured.

The following methods, among others, are employed for this:

• Principle of principal components analysis (PCA)
• Multivariate regression methods
• Multi-linear regression (MLR)
• Partial least squares regression (PLS-R)
• Principal component regression (PCR)
• Creation of multivariate calibration models for predicting unknown data